坐标系变化
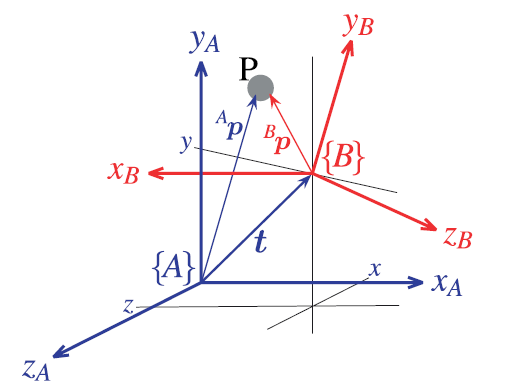
在空间中存在一点P,在坐标系A中,该点的位置可以用向量$^{A}\vec{P}$表示,如果将A坐标系变换到B坐标系,在B坐标系该点则可以表达为$^{B}\vec{P}$,这里面存在一个关系如下
$$
^{A}\vec{P}=\left(\begin{matrix}^{A}x \
^{A}y\
^{A}z
\end{matrix}\right)
=^{A}R_{B}\left(\begin{matrix}^{B}x \
^{B}y\
^{B}z
\end{matrix}\right)
$$
其中$^Bx$这些是$^{B}\vec{P}$的展开,$^{A}R_{B}$代表坐标系A到B的转换。
旋转变化
对于绕x,y,z轴旋转的变换矩阵可按下面表示,具体的推导不写了,就是将其转为2维平面的对换就知道了。这三个公式是要熟记的。 $$ R_x(\theta)=\left[\begin{matrix}1 & 0 &0 \\ 0& cos\theta&-sin\theta\\ 0& sin\theta & cos\theta\end{matrix}\right], \\\ R_y(\theta)=\left[\begin{matrix}cos\theta & 0 &sin\theta \\ 0& 1&0\\ -sin\theta& 0 & cos\theta\end{matrix}\right],\\ R_z(\theta)=\left[\begin{matrix}cos\theta & -sin\theta &0 \\ sin\theta& cos\theta&0\\ 0& 0 & 1\end{matrix}\right] $$
三次旋转连乘
Fixed Angles法 (点在{A}世界坐标系中的空间变换)
对于一个位姿,其实可以通过依次绕’世界坐标系**(这个描述很重要)**x, y, z轴旋转某些角度得到,这个旋转矩阵可以表示为 $$ ^A_BR_{xyz}(\gamma,\beta,\alpha) = R_{z}(\alpha)R_y(\beta)R_x(\gamma) $$ 其中, $$ ^A_BR_{xyz}(\gamma,\beta,\alpha) $$ 表示绕x,y,z轴分别转动$\gamma,\beta,\alpha$角度使得坐标系A到B。值得注意的是,这个的旋转顺序是先绕x轴转,再到y,再到z。那么为什么旋转矩阵的部分是zyx呢,因为这个一个旋转矩阵要乘上一个世界原始的坐标系在右边,那么按照旋转顺序,应该是x先转,那么绕x转的顺序放在最右边,依次类推。
网上的理解是这样的: 可以理解为,点$^{B}\vec{P}$先做绕X轴做$\gamma$旋转变换,得到向量$\vec v$,接着$\vec v$做绕Y轴$\beta$旋转变换,得到向量$\vec w$,最后向量$\vec w$绕Z轴做$\alpha$旋转变换,得到$^A\vec{P}$,这是一个右乘计算,公式表示为: $$ \begin{align} \vec{v}&=R_{x}(\gamma)^{B}\vec{P},\\ \vec{w}&=R_{y}(\beta)\vec{v},\\ ^A\vec{P}&=R_{z}(\alpha)\vec{w},\\ ^A\vec{P}&=R_{z}(\alpha)R_{y}(\beta)R_{x}(\gamma)\vec{P_B} \end{align} $$
这一个公式展开是 $$ \begin{align} ^A_BR_{xyz}(\gamma,\beta,\alpha) &= R_{z}\alpha)R_y(\beta)R_x(\gamma)\\ &=\left[\begin{matrix} cos(\alpha) & -sin(\alpha) & 0\\ sin(\alpha) & cos(\alpha) &0\\ 0&0&1\end{matrix}\right] \left[\begin{matrix}cos\beta & 0 &sin\beta \\ 0& 1&0\\ -sin\beta& 0 & cos\beta\end{matrix}\right]\left[\begin{matrix}1 & 0 &0 \\ 0& cos\gamma&-sin\gamma\\ 0& sin\gamma & cos\gamma\end{matrix}\right]\\ &= \left[\begin{matrix}cos\alpha cos\beta&cos\alpha sin\beta sin\gamma-sin\alpha cos\gamma&cos\alpha sin\beta cos\gamma+sin\alpha sin\gamma\\ sin\alpha cos\beta&sin\alpha sin\beta sin\gamma+cos\alpha cos\gamma & sin\alpha sin\beta cos\gamma-cos\alpha sin\gamma\\ -sin\beta&cos\beta sin\gamma&cos\beta cos\gamma\end{matrix}\right]\\ &=\left[\begin{matrix}r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33}\end{matrix}\right] \end{align} $$ 在旋转中,顺序很重要,不同的旋转顺序将导致不同位姿
逆解
如何由旋转矩阵计算各轴旋转的角度 $$ \begin{align} \text{if }\beta\neq90^o\\ \beta &= Atan2(-r_{31},(r_{11}^2+r_{21}^2)^{1/2})\\ \alpha&=Atan2(r_{21}/cos\beta,r_{11}/cos\beta)\\ \gamma&=Atan2(r_{32}/cos\beta,r_{33}/cos{\beta}) \end{align} $$ 当$90^o\leq\beta\leq90^o$时,该公式才有唯一解
ZYX Euler Angles法(坐标系{B}相对于世界坐标系{A}的空间变换)
这个方法其实就是代表着绕物体本身的坐标系(这个很重要),先绕Z轴转动,然后Y轴转动,然后X轴转动,其数学表达式为: $$ ^A_BR_{zyx}(\alpha,\beta,\gamma) = R_{z}(\alpha)R_y(\beta)R_x(\gamma) $$ 为什么这里的旋转矩阵的展开是z, y, x呢,以mapping来想,对某一个向量,从最后一个frame【逐渐转动或移动】来回到第一个frame,
因此这一个式子展开将和固定轴旋转展开的一模一样,对于位姿来说,也是一模一样的位姿
合并旋转和位移的矩阵
先转动后移动
$^AQ$移动的向量矩阵,$R_{K}(\theta)$旋转的矩阵,$^AP_1$为变换前P1在A坐标系下的向量,$^AP_2$变换后 $$ ^AP_2=R_{K}(\theta)^AP_1+^AQ $$
$$ \begin{align} R_x(\theta)&=\left[\begin{matrix}^{A}P_2\\1\end{matrix}\right]\\ &=\left[\begin{matrix}R_{K}(\theta) & ^AQ\\ \text{0 0 0} &1\end{matrix}\right] \left[\begin{matrix}^AP_{1}\\ 1\end{matrix}\right]= \left[\begin{matrix}R_{K}(\theta)^AP_{1}+ ^AQ\\ 1\end{matrix}\right] \end{align} $$
也就是把位移矩阵和旋转矩阵写进一个4x4的矩阵里
先移动后转动
$$ ^AP_2=R_{K}(\theta)(^AP_1+^AQ) $$