机械臂正向运动
DH建模
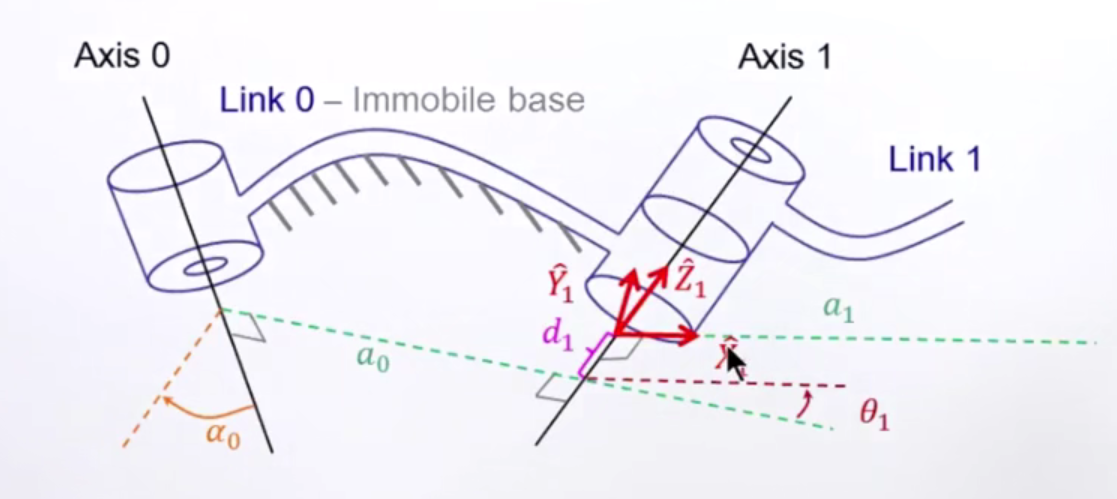
针对机械臂各个关节的姿态变化采用的是DH建模法。每个关节的都建立坐标系,而每个关节坐标系之间的关系便是通过DH的四个参数来确定,这四个参数分别是
- $a_i$: 表示的是两个连杆i和i+1的z轴之间的距离,而这z轴的确定是与转动轴重合的
- $\alpha_i$: 表示的是两个连杆i和i+1的z轴之间的角度
- $\theta_{i+1}$: 表示的是两个连杆i和i+1的x轴之间的角度,x的方向是根据与a参数同向的方向来确定
- $d_{i+1}$: 表示的是两个连杆i和i+1的x轴之间的距离

坐标转换
在确定了上面的四个参数后,其实我们可以已经计算出机械臂端的姿态在其他坐标系中的表达
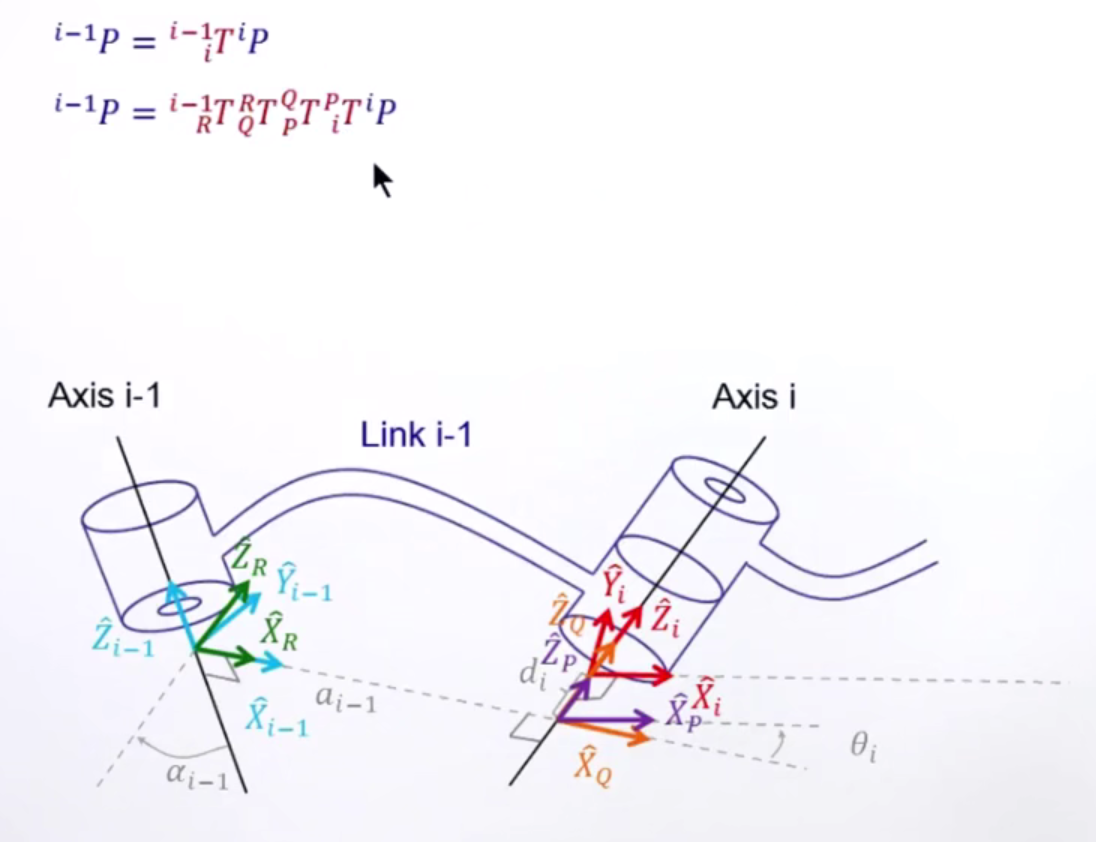
这里以两个连杆的坐标系变换来解释
首先是设定i-1的关节首先绕x轴转动,转动$\alpha_{i-1}$,这样使得Z轴与下一关节的Z轴平行,以此作为变换后的第一个坐标系R。
然后将这个坐标系平移$a_{i-1}$距离,这样使得这个坐标系与下一关节的坐标系的Z轴重合了,该坐标系记为Q。
然后再将该坐标系绕Z轴旋转$\theta_{i}$,使得X轴与关节i的方向平行,该坐标系记为P
然后再将该坐标系Q沿着Z轴方向移动$d_{i}$移动到与X轴重合,至此,两个关节的坐标系就移动到位了
所以这两者的坐标系变换矩阵就是 $$ \begin{aligned} ^{i-1}P &=^{i-1}_{R}T^R_QT^P_iT^iP\\ &=\left[\begin{matrix}cos\theta_i & -sin\theta_i & 0 & a_{i-1}\\ sin\theta_{i}cos{\alpha_{i-1}}&cos\theta_icos\alpha_{i-1}&-sin\alpha_{i-1}&-sin\alpha_{i-1}d_i\\ sin\theta_{i}sin\alpha_{i-1}&cos\theta_isin\alpha_{i-1}&cos\alpha_{i-1}&cos\alpha_{i-1}d_i\\ 0&0&0&1 \end{matrix}\right] \end{aligned} $$