雅可比矩阵(Jacobian Matrix)
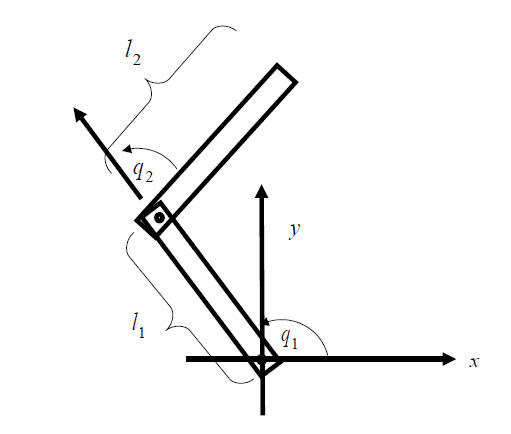
对于一个机械臂来说,比如上图,其末端点$\vec{p}$的表达式为 $$ \vec{p} = \left[\begin{matrix}l_1cos(q_1)+l_2cos(q_1+q_2)\ l_1sin(q_1)+l_2sin(q_1+q_2)\end{matrix}\right] $$ 对其位置进行q的求导得到 $$ \frac{dp}{dq} = \left(\begin{matrix}-l_1sin(q_1)-l_2sin(q_1+q_2)-l_2sin(q_1+q_2)\ l_1cos(q_1)+l_2cos(q_1+q_2)-l_2cos(q_1+q_2)\end{matrix}\right)=J(q) $$ 这个矩阵就称为这个机械臂的雅可比矩阵
对这个公式进行继续的变换可得 $$ \begin{align} \frac{dp}{dq}&=J(q)\ dp &=J(q)dq \end{align} $$ 不难发现dp是位置的导数即速度,dq是角度的导数即角速度
雅可比矩阵下的逆解也很好理解

https://nrsyed.com/2017/12/10/inverse-kinematics-using-the-jacobian-inverse-part-2/