轨迹规划
轨迹的规划方式有两种,一种是在joint-space下进行,一种是在Cartesian-space下进行。
Joint-space
Joint-space的思想是,首先运动学逆解求解出当前机械臂各个关节的角度,和最终目标位姿时各个关节的角度,然后针对这两组关节角度规划一条平滑的曲线,然后再通过运动学正解来验证轨迹的可行性,因为可能存在障碍物的阻碍。
-
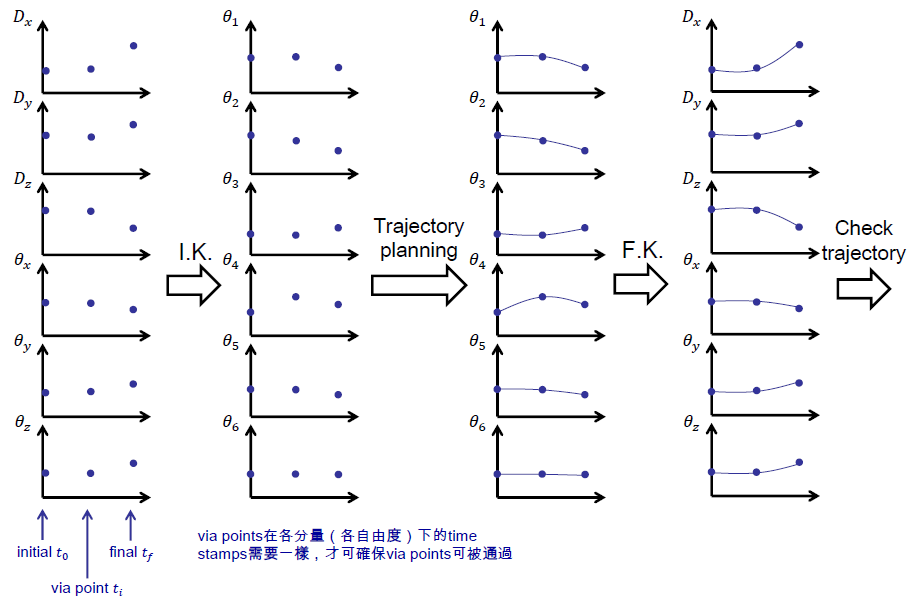
定义这段轨迹在空间中的起始点{$t_{0}$},中间点{$t_i$}以及终点{$t_f$}。
-
计算这些点的IK,得到在每个时间点titi,手臂的每个joint所对应的角度。
-
对每一个joint都在其自己的角度坐标系下规划一条平滑的曲线。
-
计算FK,检查手臂末端点在Cartesian-space下轨迹的可行性(可能会碰到障碍物)
Cartesian-space
这个方法是用的比较多的方法。这个方法首先直接根据当前位姿和目标位姿规划出平滑的轨迹曲线,然后再运动学逆解求出关节角度,再检查各个关节轨迹的可行性。由于要计算整个轨迹点的运动学逆解,因此计算量大
-
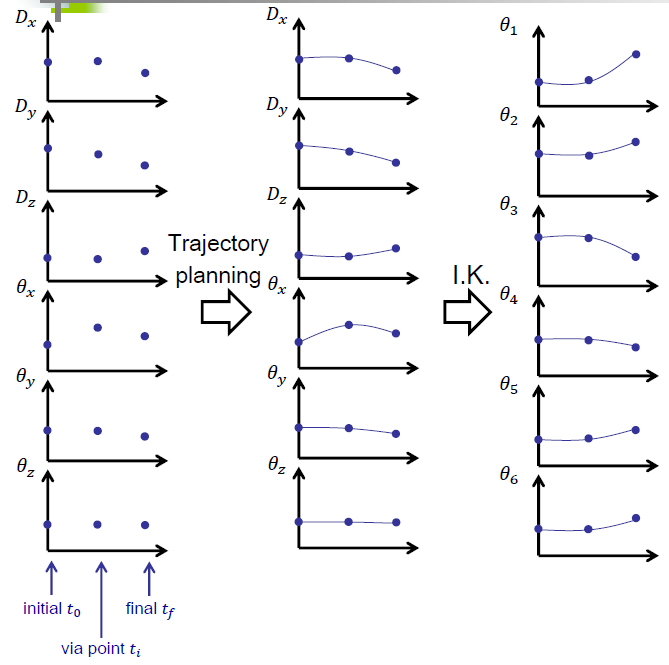
定义这段轨迹在空间中的起始点{$t_0$},中间点{$t_i$}以及终点{$t_f$}。
-
对每一个手臂末端点的状态参数(x,y,z,$θ_x$, $θ_y$ , $θ_z$)规划一条平滑的曲线。
-
将规划好的手臂末端点状态的轨迹点计算IK,转换到joint-space下。
-
检查joint在joint-space下轨迹的可行性(有的joint的转动角度有限制或者角加速度太大手臂做不到)
如何规划曲线
规划平滑的曲线有两种方式,一种是基于一个三次多项式来规划的,和
Cubic Polynomials
通过一个三次多项式来描述一个区段内点的轨迹 $$ \theta(\Delta t)=a_0+a_1\Delta t+a_2\Delta t^2+a_3\Delta t^3 $$ 其中,$a_0$到$a_3$这四个就是高阶项的参数,也就是一个线性模型罢了,每一个区段[$t_i$, $t_{i+1}$]都有一个这样的三次多项式,只不过每段的参数不同。$\Delta t$就是时间差,对于每一个区段t$\in$[$t_i$, $t_{i+1}$],$\Delta t = t - t_i$,所以当$t = t_i$时$\Delta t=0$
这是一个含有四个未知数的多项式
增加边界条件
首先考虑$t=t_i$和$t=t_{i+1}$时,这个三次多项式为 $$ \theta(\Delta t|{t_i})=\theta_i=a_0 $$ $$ \theta(\Delta t|{t_{i+1}})=\theta_{i+1}=a_0+a_1\Delta t+a_2\Delta t^2+a_3\Delta t^3 $$
对$\theta$求导,便是速度了,我们也需要对速度进行设计,这样才能保障路径平滑 $$ \frac{\partial \theta(\Delta t|{t_i})}{\partial\Delta t}=a_1 $$ $$ \frac{\partial \theta(\Delta t|{t_{i+1}})}{\partial\Delta t}=a_1+2a_2\Delta t+3a_3\Delta t^2 $$
联立这四个方程最后可得
$$
a_2 = \frac{3}{\Delta t^2}(\theta_{i+1}-\theta_i)-\frac{2}{\Delta t}\dot{\theta_{i}}-\frac{1}{\Delta t}\dot{\theta_{i+1}}\
a_3 = -\frac{2}{\Delta t^3}(\theta_{i+1}-\theta_i)+\frac{1}{\Delta t^2}(\dot{\theta_{i+1}}+\dot{\theta_i})
$$
以矩阵的方式来表达

下图这个是多段三次多项式的通解,两个$\theta_1$其实是一样的,但是需要写出来

多段三次多项式通解
假设一共有N+1个点,其中有1个初始点,N-1个中间点和1个终点。那么我们一共就有N个三次多项式,每个三次多项式有4个未知参数,所以一共有4N个未知量。为了求解这4N个未知量,我们就需要4N个限制条件:
- 每一段会有两个位置条件,所以一共有2N个位置条件;
- 每一个中间点会有一个速度条件和一个加速度条件,所以一共有2(N-1)个速度和加速度条件;
- 目前为止一共有4N-2个条件,那么最后两个条件我们可以限制起始点和终点点的速度或者是加速度,这样就有4N个条件了。
高阶多项式
如果我们不但要规划位置和速度,还要规划加速度的话,我们就需要用到五次多项式,而不是四次多项式。因为位置、速度和加速度分别会产生2个条件,一共有6个条件,五次多项式有6个未知数。

参考:https://xiaobaidiy.github.io/2020/05/13/robot-arm-5/